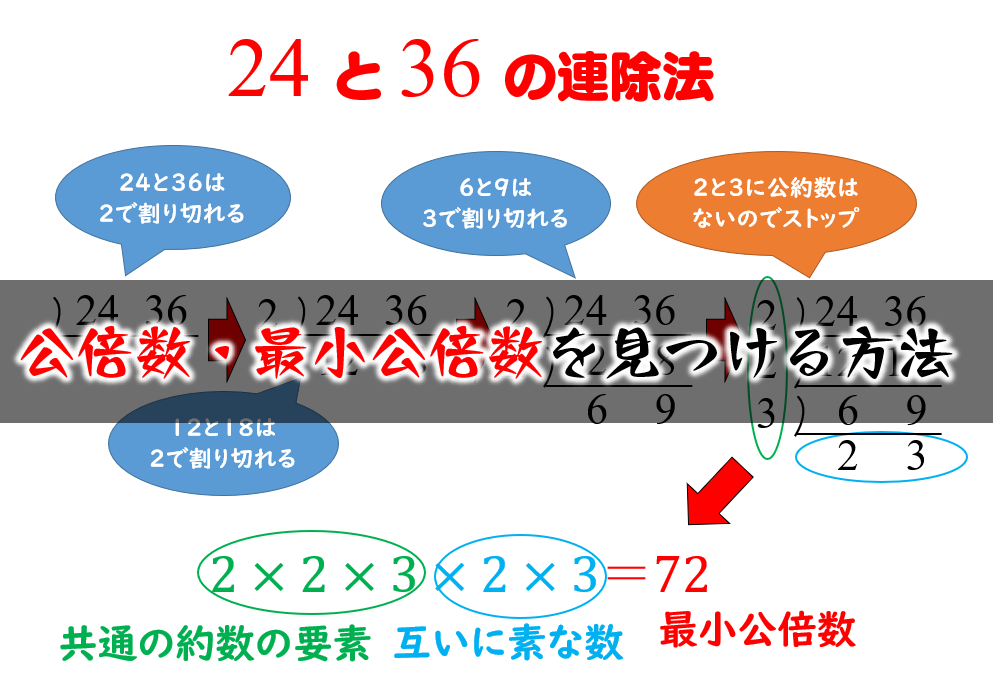
詳細な解法を提供する Microsoft の無料の数学ソルバーを使用して最大公約数について学習しましょう。 (,32) g c f (2 0, 3 2) gcf(100,40) g c f (1 0 0, 4 0) gcf(105,55,30) g c f (1 0 5, 5 5, 3 0) クイズ 次に類似した 5 個の問題 gcf(12,16) g c f (1 2, 1 6) 次に類似した 5 個の問題ここでは、「公約数(こうやくすう)」と「最大(さいだい)公約数」を考えよう。 「約数」と「公約数」の違いは、「公」っていう漢字が付いていることだね。 「公」は「おおやけ」って読めるね。 「公」の意味は「全体」だね。 ちなみに、「公」の反対の言葉は「私」だね。 「公的」の反対の言葉で「私的」って使うよね。 「公」の意味は「全体」って最大公約数 を求める1つの方法は,共通な数で割れるだけ割っていく方法です. このとき,共通に割れる数の積が最大公約数です. 最小公倍数 を求める方法は,これと同様ですが,割った数と残った数を掛けます. 例 次の例で, 12 , 18 の最大公約数は 6

小学生 3つの数の最小公倍数 最大公約数の求め方 特殊なすだれ算も図で解説 中学受験 そうちゃ式 受験算数 新1号館
16と20の公約数
16と20の公約数-データセットの数は 1000 を超えません。 Output データセットごとに、入力された2つの整数の最大公約数と、計算にかかったユークリッドの互除法のステップ数を空白区切りで1行に出力します。 Sample Input 1071 1029 5 5 0 0 Output for the Sample Input 21 3 5 1三角数が三角数になる約数の個数をもつ数の中で前の数を上回る個数をもつ4番目の数である。1つ前は496、次は。(オンライン整数列大辞典の数列 a) 16 = 741 1275 三角数が異なる2つの三角数の和で表せる38番目の数である。1つ前は1953、次は80。
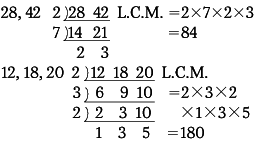



最小公倍数とは コトバンク
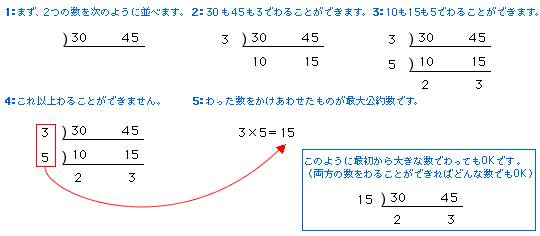
・6と9の公約数:1、2、4 12と16の最小公約数はいくつだと思いますか。 公約数のうち、もっとも小さい数の「1」ですよね。 ここで気がついたひともいるのではないでしょうか。 「最小」公約数だと、どのような数でも「1」になってしまうのです。1.次の数の約数を全て書きましょう。 ① 5 ④ 27 ② 10 ⑤ 48 ③ 16 ⑥ 72 2.次の( )の中の数の公約数を全部書きましょう。 ① (9 ,27) ② (8 ,16) ③ (36 ,54) ④ (12, 36 ,54)2つの数があり、両方の数の約数になっている数を「公約数」といいます。 公約数の中でいちばん大きい数を「最大公約数」といいます。 約数、公約数、最大公約数 は、分数のたし算・ひき算でよく使う言葉ですので、しっかり覚えておきましょう。
16 の約数 1, 2, 4, 8, 16 24 の約数 1, 2, 3, 4, 6, 8, 12, 24 二つの数の約数が全部出てきました。共通する約数は 1, 2, 4, 8 です。よって最大公約数は 8 となります。 最小公倍数の計算 続いて最小公倍数を求めてみましょう。最小公倍数は元の数をかけたものを最大公約数で割ると求まります。16 と 24 の最小公倍数は 16 × 24 ÷ 8 = 48 となります。 結論 最大公約数:8 最小公Q最大公約数を求めましょう。 ①(16,) ②(28,56) ③(,60) の求め方と 答えを教えてくださぃ。 2つの元となる数とそれらの最大公約数と最小公倍数には、ある関係性があります。 『2つの元となる数の積』と『最大公約数と最小公倍数をかけた数』は同じ数になるということです。 例えば、 元となる数を と30にすると と30 の最大公約数 = 10 と30 の最小公倍数 = 60 × 30 = 600 10 × 60 = 600 このように同じ数になります。
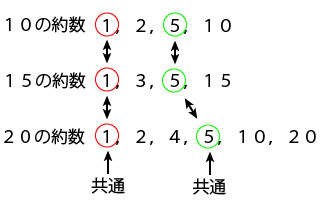
③ (8 16 ) 3 ( )の中の数の公約数をすべて求めましょう。 ① (12 18) ② (18 36) 2 次の数の約数をすべて求めましょう。2つの数のそれぞれの約数のうち、共通する約数のことを 公約数 (こうやくすう)と言います。 10の約数 1 2 5 10 15の約数 1 3 5 15 赤の数字が共通する約数です。 なので10と15の公約数は「1と5」と幾つか試してみるとわかるように,ユークリッドの互除法を使えば最大公約数が数回の割り算で求められます.しかし,商が1( A=BR )となる組ばかりになる場合には,なかなか数字が減っていかないので,長~い計算を要することとなります. すなわち



約数とは 約数の個数や総和の求め方 約数表 計算問題 受験辞典



最小公倍数の2通りの求め方 3つの場合も 具体例で学ぶ数学
まずは 16 と の約数を求めてみましょう。 16 の約数: 1、2、4、8、16 の約数: 1、2、4、5、10、 二つの数の約数がわかったので、共通する約数は 1, 2, 4 とわかります。 したがって最大公約数は 4 となります。次の数の最大公約数を書きましょう。 ① 16, ( 4 ) ② 9,45 ( 9 ) 24本の赤い花と36本の白い花を,それぞれ同じ本数ずつあまりのないように テーマ: 計算 約数とはある数を割り切ることのできる数のことをいいます。 例えば、24の約数は、1・2・3・4・6・8・12・24 となるわけです。 ちなみに13のように1とその数自身しか約数がないものを素数といいます。 この約数が2つ以上の数の約数になるときは、それらの数の公約数というのです。 12と16の公約数といったら、1・2・4 となることは理解できます




12 と の最小公倍数を求めよ ブログ さいたまキャンパス 鹿島学園高等学校 通信制高校 カシマの通信



16 と の 公約 数 シモネタ
最大公約数 (GCD)を簡単に求める計算プログラムです エクセルじゃないですが、最大5つの数に対して計算可能です 入力値は最大5桁までの整数に限ります(負荷の関係で適当に制限かけてます) 入力値が「0」の場合は無視します 計算 数値を入力して下さい * available language en ja pt es zhTW zhCN th 1からまでの数の最小公倍数がだとわかってよかった 1519 男/歳未満/小・中学生/役に立った/ 使用目的 4861と25の最大公約数 ご意見・ご感想 確認のためにできてよかった 1547 男/歳代/高校・専門・大学生・大学院生/役に立った/ 使用目的「16、36」の2数の公約数を求めてください。また、公約数の数はいくつでしょうか。 >公約数(2数)の演習問題 No32 下記のページには、つぎのような公約数(2数)の演習問題が問あります。 「72、64」の2数の公約数を求めてください。



公約数と公倍数 わかる数学




16 24 を素因数分解して この3つの数の Clear
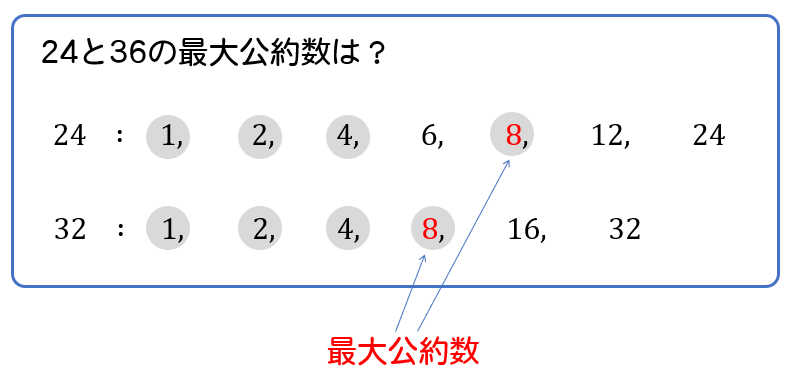
16の約数 = 1, 2, 4, 8, 16 24の約数 = 1, 2, 3, 4, 6, 8, 12 両方に共通する約数 = 1, 2, 4, 8 よって、16と24の公約数は1, 2, 4, 8。 4人 がナイス! しています2つの異なる自然数a,bの共通の約数を、a,bの( 公約数 )という。 最も大きい公約数を( 最大公約数 )といい、24と36の最大公約数は( 12 )である。 <問題3> 2つの自然数の公約数は、最大公約数の約数であることを上の例題で確認せよ。16と24の公約数 ⇒ 1、2、4、8 12との公約数 まずは12との約数を求めます。 12の約数 ⇒ 1、2、3、4、6、12 の約数 ⇒ 1、2、4、5、10、 12との公約数 ⇒ 1、2、4 24と36の公約数 まずは24と36の約数を求めます。 24の約数 ⇒ 1、2、3、4、6、8、12、24 36の約数 ⇒ 1、2、3、4、6、9、12、18、36 24と36の公約数 ⇒ 1、2、3、4、6、12 4と10の公約数




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生



1
16 1,2,4,8,16 17 1,17 * 18 1,2,3,6,9,18 19 1,19 * 1,2,4,5,10, 21 1,3,7,21 22 1,2,11,22 23 1,23 * 24 1,2,3,4,6,8,12,24 251 次の数の約数を全部かきましょう。 ① 8 ② 9 ③ 12 ④ 15 ⑤ 45 ⑥ 60 2 ( )の中の数の公約数を全部かきましょう。 ① (12,) ② (16,24) ③ (27,36) ④ (48,12) 約数と公約数 組 名前 月 日 ⑤ 11 第回約数と公約数③(素数と素因数分解)の授業プリント&授業映像 更新日: 21年4月16日 第回約数と公約数③(素数と素因数分解)の授業プリントはこちらから印刷できま




1 A 0 12 2 16 3 6 6 8 Lihat Cara Penyelesaian Di Qanda




小学生 3つの数の最小公倍数 最大公約数の求め方 特殊なすだれ算も図で解説 中学受験 そうちゃ式 受験算数 新1号館
例題1: 次の倍数を,小さい方から 9 個求めなさい。 (1) 4 の倍数 (2) 6 の倍数 答え: (1) 4 の倍数 → 4, 8, 12, 16, , 24, 28, 32, 36 (2) 6 の倍数 → 6, 12, 18, 24, 30, 36, 42, 48, 54 解説は別になくてもOKですね。 次ページの,例題2に進んでください。 例題1で,最後の演習問題は、ユークリッドの互除法を用いて、最大公約数を求めるというものでした。 → (,36をで割った余り) =(,16) → (16,を16で割った余り) =(16,4) → (4,16を4で割った余り) =(4,0) ↑ この4が128と36の最大公約数符号付き16ビットで表せる正の整数の数である。 2 16 = 65,536 16ビットで表せる整数の数である。Intel 8086などが16ビットである。 4 2、2↑↑4(矢印はクヌースの矢印表記)のテトレーション数である。 2 = 1,048,576 に最も近い2の累乗数である。




教材出版 学林舎 成長する思考力gtシリーズ制作 販売



公倍数 最小公倍数 Youtube
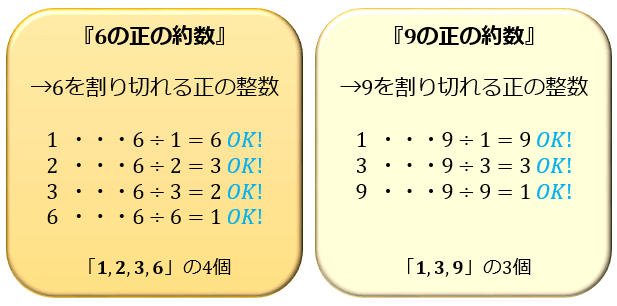
72の約数は1、2、3、4、6、8、9、12、18、24、36、72の12個。 (2) 101、103、107となるので、107。 (3) 右の解法により13×2=26。 (4) 右の解法により2×2×2×3×5×8=960。 (5) 144の約数は1、2、3、4、6、8、9、12、16、18、24、36、48、72、144でこの、1,3,5,15を「15と45の公約数」といいます。 ③ 最大公約数2つ以上の整数に共通な約数(公約数)のうち、 最大のものをいいます 例1. 8の約数は、1,2,4,8です。 12の約数は、1,2,3,4,6,12です。最小公倍数 (LCM)を簡単に求める計算プログラムです 最大5つの数に対して計算可能です 入力値は最大5桁までの整数に限ります(負荷の関係で適当に制限かけてます) 入力値が「0」の場合は無視します 最大公約数を求めるアプリ 計算 数値を入力して



3




式 と答えお願いいたします Clear
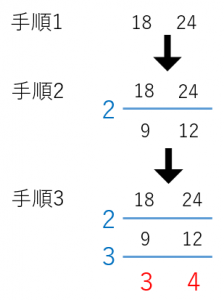
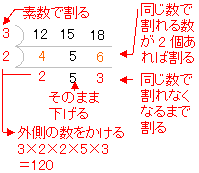
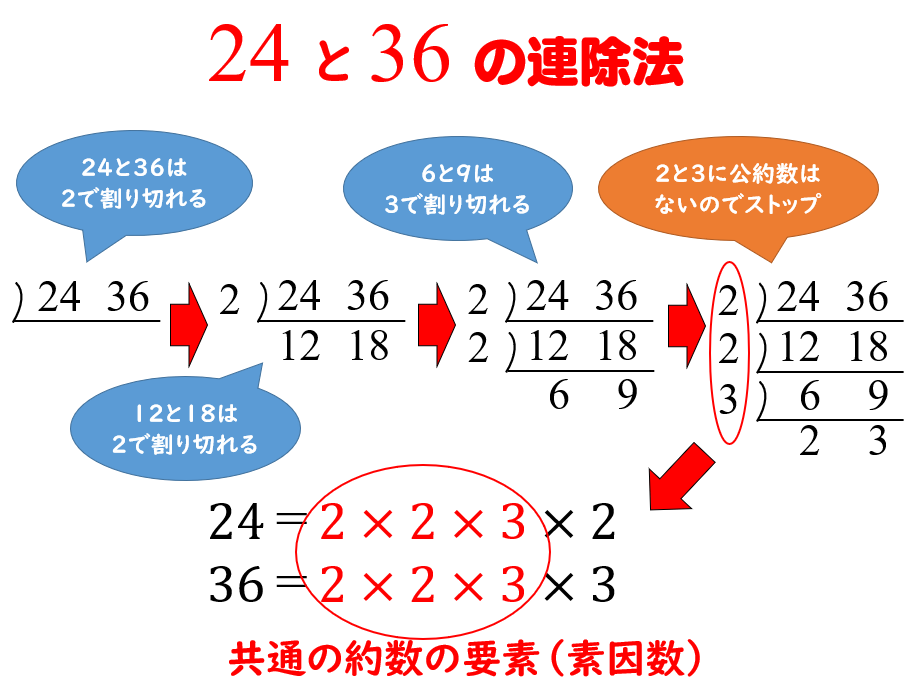
約数と倍数③ 最大公約数と最小公倍数とは 12と18の公約数は、1, 2, 3, 6, の4つでしたね。 最大公約数とは、この4つのうちいちばん大きいものです。 つまり6。使用目的 最小公倍数 ご意見・ご感想 1,2,3,4,5,6,7,8,9,10,11の最小公倍数を求めるのに使用。 結果、277。 マスの数がデフォルトでは2個。 マスをまとめて10個くらい追加出来ると嬉しいけど、そんな用途は少ないのかな。 先日は30個以上で計算。 4 1516 歳未満 / 小・中学生 / 非常に役に立った /16の約数・・・1,2,4,8,16 だから12と16の公約数は、1,2,4である。 12と18に共通な約数がある! 整数が3つになっても、やるこ とは一緒!3つの整数に共通な 約数を探してかこう! 公約数のうち、一番大きい公約数のことを最大公約数という。(今回の



Http Www City Hadano Kanagawa Jp Www Contents Simple A036a Pdf



約数とは 約数の個数や総和の求め方 約数表 計算問題 受験辞典
16桁の合成数: = × 概要 1京未満 (16桁以下) の自然数について、素数かどうか判定するツールです。⑵ と30の公約数を求めます。公約数は,最大公約数の約数ですから, 右の連除法より,最大公約数は(2×5=)10です。よって, 整数aは10の約数である,{1,2,5,10}になります。 答 ⑴3個 ⑵1,2,5,10 トレーニング1 ⑴ 次の数の約数はそれぞれ何個あり



最大公約数の求め方 すだれ算 中学受験 塾なし の勉強




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 への道



16 と の 公約 数 シモネタ




8 1 812 N 3 4 6 12 12 81 Descubre Como Resolverlo En Qanda




最大公約数 Wikipedia



最大公約数教えてください35と1496と5616と2032と4872人は Yahoo 知恵袋



2




宿題です どこが間違っているか教えて下さい Clear



約数 公約数 最大公約数 算数の教え上手 学びの場 Com



2




この4問教えてください Clear



倍数 公倍数 最小公倍数 通分 分数のたし算ひき算の授業 教材 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 への道




整数の性質 倍数の見分け方 最大公約数と最小公倍数 富岡市の総合学習塾 トータルアカデミー



約数 倍数




C 最大公約数 最小公倍数を求める はなちるのマイノート




公約数と公倍数の練習問題を解いてみましょう 分数の計算をするために 必要ですので 考え方をよく理解した後は たくさん練習をして 速く正確に答えられるようにしていきたいですね 公倍 学習ノート 学習 分数
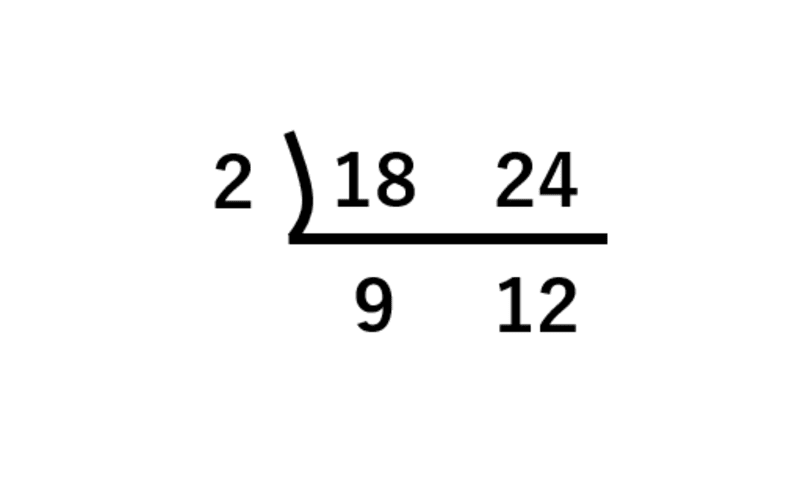



算数の公約数 最大公約数を完全解説 簡単な求め方や計算方法 センター試験対策も紹介 学びtimes



2



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ
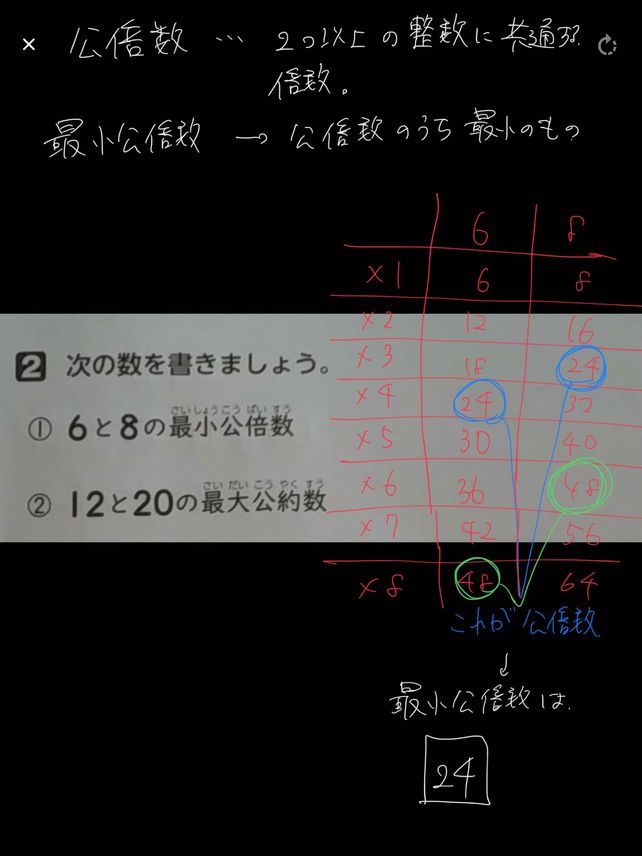



2 6 8 12 Descubre Como Resolverlo En Qanda
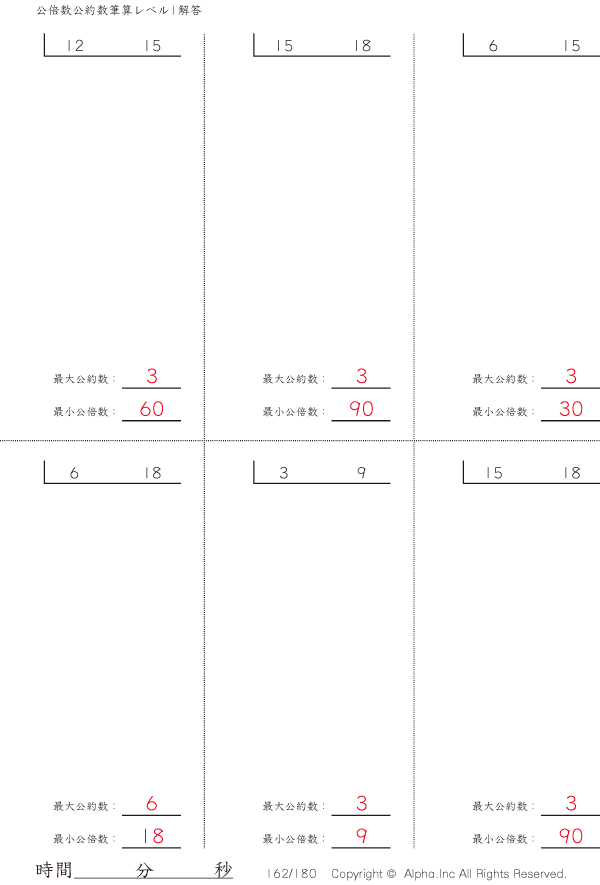



公倍数公約数の筆算 レベル1 解答 162 180



倍数と約数 最小公倍数 最大公約数のひみつ



倍数と約数 最小公倍数 最大公約数のひみつ シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




最小 公約 数 と は 最大公約数と最小公約数の違いを教えてください具体的の方が助かりま Amp Petmd Com



Tarcsquare Lihat Cara Penyelesaian Di Qanda
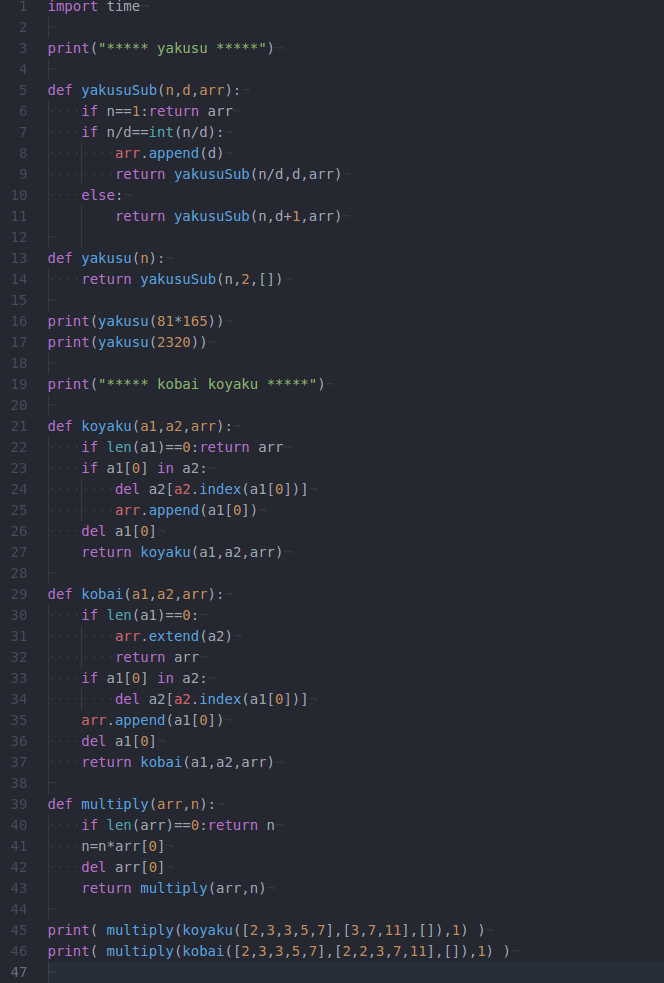



38 再帰 Pythonで約数を求める パーソナルブログメモリ




倍数と約数 最小公倍数を求める 問題練習 Youtube



2




公約数の求め方 もう一度やり直しの算数 数学
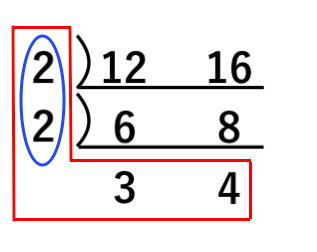



最大公約数と最小公倍数のひみつ 苦手な数学を簡単に



2




公倍数




公倍数



倍数 公倍数 最小公倍数 通分 分数のたし算ひき算の授業 教材 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



5年算数整数 教え方のポイント



2



5年算数整数 教え方のポイント



2




最小公倍数の計算 自動計算サイト



最小公倍数とは コトバンク
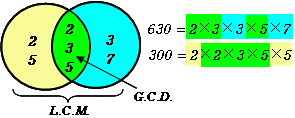



最大公約数と最小公倍数 高精度計算サイト




3分で分かる 最小公倍数とは 4通りの求め方も紹介 合格サプリ



約数 公約数 最大公約数 約分 分数のたし算ひき算の授業 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



Fdk3a7ctb5192box5b Com Es 5nen Mt Yakusu Html




約数 公約数 最大公約数 算数の教え上手 学びの場 Com



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ



16と24の公約数を教えてください どんなに考えてもわかりません 公 Yahoo 知恵袋



分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun




16 と の 公約 数 シモネタ




最小公倍数や最大公約数が苦手 石原清貴の算数教育ブログ



Http Www Dainippon Tosho Co Jp Newsletter Files R2 Rabichan Print5a Pdf



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun



2




24と30の最大公約数や公約数全部は 24と32の最大公約数や公約数全部は ウルトラフリーダム




世界一分かりやすい算数 小5 整数



最大公約数 Geogebra




オンライン学習会 今日は最大公約数です たぶお Sapix サピックス A1 への道




最大公約数と最小公倍数の求め方 2つの組 Youtube



1




このイメージで理解 最大公約数 最小公倍数 とまコの泥だらけお受験日記 byシンママかぶラ




中学数学より4 教科書に登場しない最小公倍数 最大公約数 身勝手な主張



公約数の求め方 もう一度やり直しの算数 数学




大きな数の最大公約数の求め方 Youtube



Http Www Collegium Or Jp Kutomi Pdf Syo Koubaisuu Kouyakusuu Answer Pdf



大きな数の最小公倍数の求め方 Youtube



数学aの問題なのですが 45 75 270の最大公約数 最小公倍数を求 Yahoo 知恵袋



1
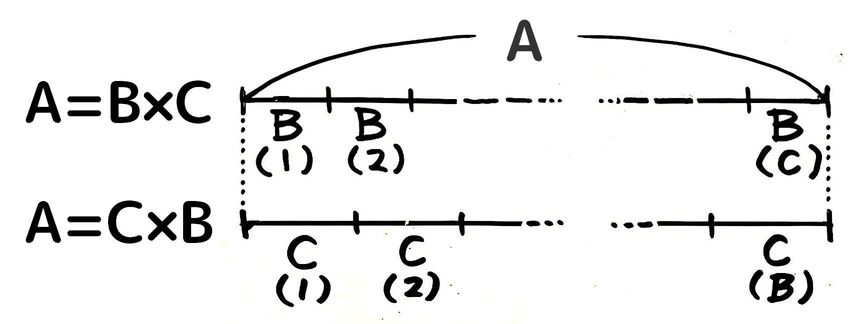



小学5年生 約数 公約数の意味と求め方は 書き出し式 プリントあり そうちゃ式 分かりやすい図解算数 別館




倍数と約数 小5 公倍数 公約数 手探るは最強の解き方 算数の教え方教えますmother S Math Happy Study Support



Fdk3a7ctb5192box5b Com Es 5nen Mt Yakusu Html




数学i Aチェック リピート 第8章 2独立試行 反復試行 2 さいころ投げ Pukiwiki



16 と の 公約 数 シモネタ



2



2



Http Www Min San Com Pd Z4 21 1 Kai




最大公約数と最小公倍数のひみつ 苦手な数学を簡単に



小学6年の計算ドリル 公約数 をやってみた まるみた Com




ブルーブリッジカップ 等差数列 Gcd 最大公約数の問題 コードワールド




高校数学a 最大公約数と最小公倍数の定義 受験の月



最大公約数 中学受験生のための瞬間反射プリント2 Wisardnet 中学受験算数を攻略する教材サイト
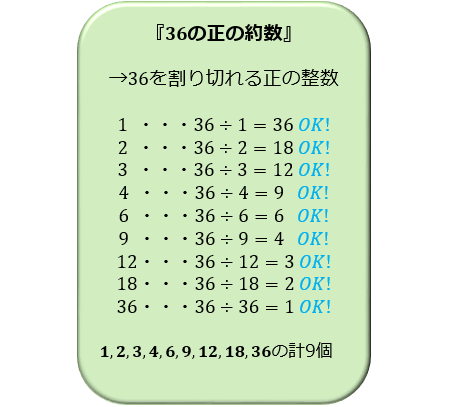



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ
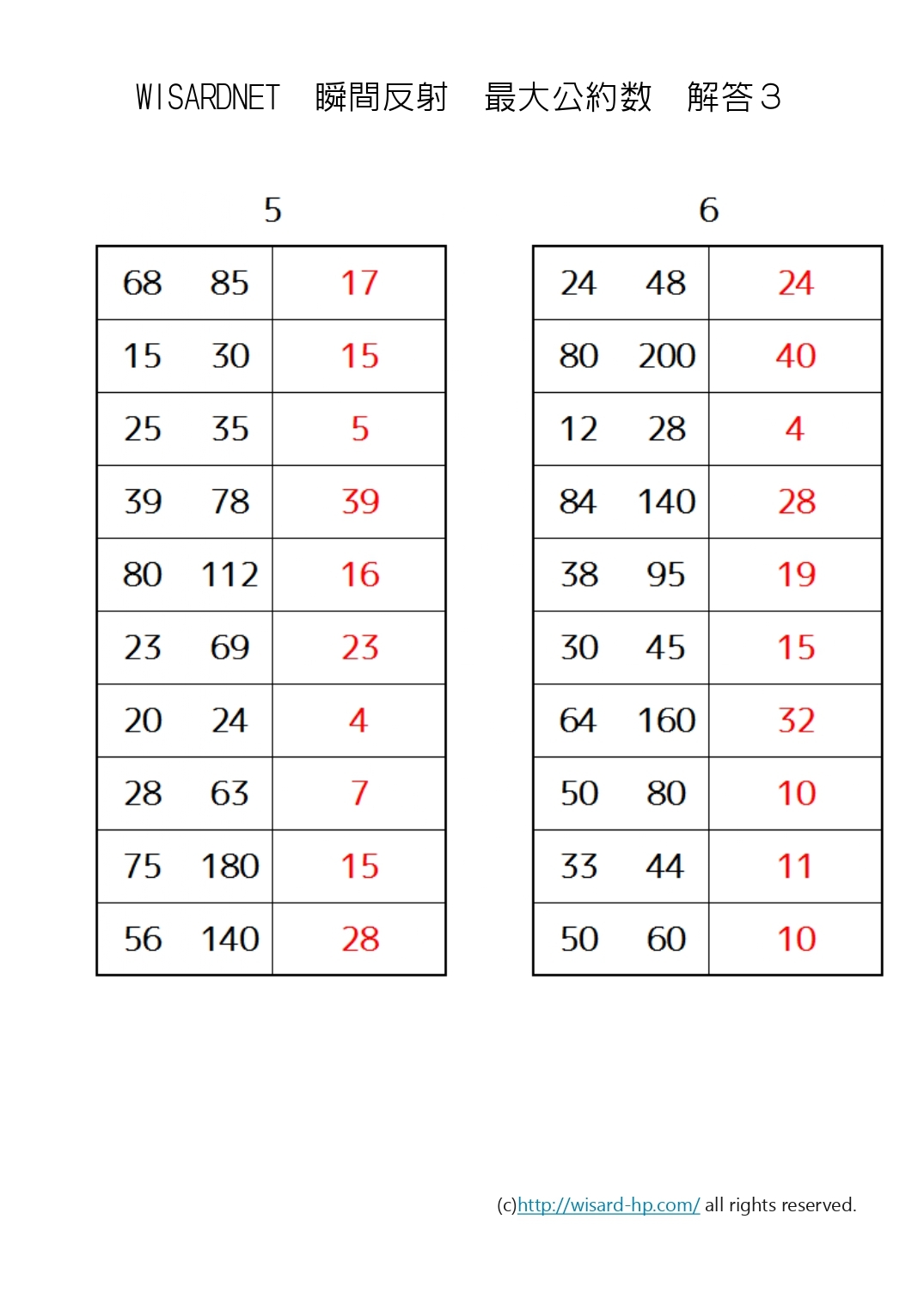



最大公約数 中学受験生のための瞬間反射プリント2 Wisardnet 中学受験算数を攻略する教材サイト



10との最大公約数 16と40と56の最大公約数を教えて Yahoo 知恵袋



Http Www Ogisin Com Shin5nensansuukaisetsub Pdf




最大公約数と最小公倍数の簡単な求め方 3つの場合も解説しています




最大公約数を求める練習問題 計算ドリル 問題集 数学fun




世界一分かりやすい算数 小5 整数



0 件のコメント:
コメントを投稿